É preciso que façamos uma pequena recapitulação da definição de probabilidade antes de desenvolvermos este módulo, onde trataremos das origens e principais propriedades da probabilidade. A probabilidade é uma técnica estatística utilizada para expressar a chance de ocorrência de um determinado evento.

A forma clássica de calcular a probabilidade é através da relação entre o número de casos favoráveis e o número de casos possíveis. Os casos favoráveis são aqueles resultados que se desejam acontecer; já os casos possíveis são todos os elementos que compõem o espaço amostral.

Sendo assim, dado um determinado espaço amostral , a probabilidade de um dado evento A, P(A), será uma função definida em , onde cada evento estará associado a um número real, a fim de satisfazer os axiomas abaixo:

1. Origens da Probabilidade

Na realidade, existem três maneiras diferentes de se calcular ou estimar as probabilidades. São eles os métodos clássico, empírico e subjetivo, sendo que os métodos clássico e empírico são considerados métodos objetivos.

1.1. Métodos Objetivos

Método Clássico

Quando estamos diante de experimentos que têm resultados igualmente prováveis, aplica-se o chamado método clássico. Neste caso, a probabilidade de ocorrer cada evento (resultado) é uma função do número de resultados possíveis.

Por exemplo, no experimento em que lançamos um dado, ocorrer qualquer das faces neste lançamento é igualmente provável. Então qual seria a probabilidade de ocorrer qualquer destas faces?

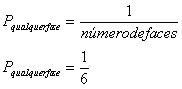
Ora, se aplicamos o método clássico a experimentos que envolvam dois ou mais resultados associados, com igual probabilidade de ocorrência destes resultados, teremos a definição clássica de probabilidade que demos no início deste módulo, onde a probabilidade será:

Por exemplo, a probabilidade de obter 4 ases num baralho de 52 cartas. Neste caso, teremos que identificar o número de resultados favoráveis, ou seja, aqueles resultados que desejamos que aconteçam. No caso, são 4 resultados favoráveis, dentro de quatro resultados possíveis, então teremos:

Isto significa que se houver uma repetição significativa deste experimento, ou seja, de se retirar 4 ases de um baralho de 52 cartas, um evento como este, que tem probabilidade de 7,6% ocorrerá em 7,6% das vezes.

Chance

Existe uma maneira diferente de se exprimir as probabilidades, ao invés de se comparar o número de casos favoráveis ao número de casos possíveis, compara-se o número de resultados favoráveis ao número de casos desfavoráveis. Isto pode ser expresso das duas formas abaixo:

ou Chance = número de resultados favoráveis : número de resultados desfavoráveis

Assim, por exemplo, numa sala de aula, temos de um total de 50 alunos, 22 homens e 28 mulheres. Qual seria, então, a probabilidade e a chance a favor de se selecionar, aleatoriamente desta sala, uma mulher?

Probabilidade:

A probabilidade de se retirar uma mulher é, portanto, de 56%.

Chance:

Evento A: selecionar uma mulher

 ou 14:11

As chances de se retirar uma mulher da sala são, portanto, de 14 para 11.

Método Empírico ou Freqüencial

Quando tratamos de situações onde os resultados não são igualmente prováveis, podemos tentar estimar as probabilidades, obtendo alguns dados empíricos. Eu tenho portanto, uma estimativa das probabilidades baseada justamente nestes dados empíricos, que serão obtidos por meio de experimentos aleatórios ou através de dados históricos. É importante ressaltar que neste caso a probabilidade será uma estimativa do verdadeiro valor.

Por exemplo, se tivermos um experimento em que lançamos um dado 100 vezes. Se destas 100 vezes, obtivermos a face 4 em 40 vezes, num próximo lançamento do dado seria razoável supor que a probabilidade estimada futura da face 4 como sendo , se este experimento se der a condições idênticas.

Da mesma maneira, quando testo uma vacina em um grupo de 1000 pessoas, por exemplo, e a vacina apresenta sucesso em 700 delas, se eu repito o teste, devo esperar uma probabilidade estimada de sucesso futuro da vacina , sob condições idênticas para a ocorrência deste resultado. Sendo assim, podemos calcular a estimativa da probabilidade de um evento futuro baseado no método empírico através da seguinte fórmula:

Se, por outro lado, ao invés de dispormos da possibilidade de obter os dados amostrais através da realização de um experimento, dispomos de dados históricos em uma distribuição de freqüência, ou na forma de dados publicados, ou como resultado de testes prévios, ou como informações que foram acumuladas em algum arquivo importante, podemos também calcular a probabilidade estimada pelo método freqüencial.   Mas para isto é preciso que partamos da premissa que o passado é representativo do futuro.

Por exemplo, suponhamos que uma distribuidora de chocolates acompanha suas vendas durante 90 dias. O objetivo desta distribuidora seria projetar as vendas para o futuro a fim de planejar seus estoques. Deste acompanhamento resultou a distribuição de freqüência abaixo:

Número de Chocolates Vendidos, Em Kg, Em um Período de 90 Dias
Quilos Vendidos	Número de Dias
20	10
30	20
40	20
50	30
60	10
Total	90

Neste caso, também poderemos adotar o método empírico, procurando determinar qual o percentual de vezes que ocorreu tal evento. Por exemplo, em 20 dias, o distribuidor de chocolates vendeu 40 quilos de chocolate em 20 dias dos 90 dias totais de nossa observação. Então, neste caso, a estimativa de probabilidade desta ocorrência é . A probabilidade é, portanto, a partir do método empírico, uma proporção da ocorrência de um evento ou a freqüência relativa do evento. Assim, para as demais classes, as probabilidades serão dadas como segue na tabela abaixo da distribuição de freqüências, seguindo agora a seguinte fórmula:

Número de Chocolates Vendidos, Em Kg, Em um Período de 90 Dias
Quilos Vendidos	Número de Dias	Probabilidade
0	10
30	20
40	20
50	30
50	10
Total	90

Algumas observações são importantes de serem ressaltadas quando utilizamos o método empírico para calcular a probabilidade.

• Quando se calcula a probabilidade a partir do método empírico obtemos apenas uma estimativa do verdadeiro valor da probabilidade. Não temos dados suficientes para determinar o valor exato da probabilidade.
• O tamanho da amostra é fundamental para determinar a estimativa da probabilidade. Quanto  maior o número de observações, e portanto, a amostra, melhor a estimativa da probabilidade.
• A probabilidade só é válida para um conjunto de condições idênticas àquelas geradoras dos dados amostrais.

1.2. Método Subjetivo

Nos itens anteriores nos propusemos a calcular probabilidades que se originavam de fatos, fosse através do método clássico ou do método empírico. No entanto, ao longo do estudo da estatística surgiram diversas situações onde os eventos não eram nem passíveis de um estudo objetivo e muito menos eram igualmente prováveis. Neste caso, então, faz-se necessário atribuir-se subjetivamente uma probabilidade. Por exemplo:

Você encontrará o amor da sua vida amanhã?
Quando os operários do metrô farão nova greve?
Uma mulher com câncer de mama se recuperará completamente?

Nestes casos, mesmo que não seja possível efetuar o experimento, pode-se imaginar um grande número de situações idênticas e questionar-se qual será o percentual destas situações que produzirá o evento desejado.
O método subjetivo é semelhante ao método empírico, a única diferença é que em geral os dados não podem ser coletados. A probabilidade subjetiva serve como um esforço não apenas para quantificar, mas para confirmar nossa crença a respeito de algo.
A definição clássica de probabilidade subjetiva é a que segue:

Probabilidade subjetiva é uma avaliação pessoal do grau de viabilidade de um evento

Existem, obviamente, algumas desvantagens importantes que este método apresenta:

1. As estimativas subjetivas são em geral difíceis de defender quando postas em dúvida;
2. As estimativas subjetivas podem ser tendenciosas.

 

2. Principais Teoremas de Probabilidade

I) Digamos que temos um evento A qualquer, e um conjunto  que representa o conjunto vazio. Suponhamos ainda que A e sejam disjuntos, então teremos:

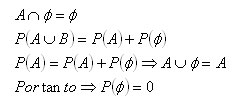
Sendo assim, temos que o primeiro teorema importante de probabilidade é o seguinte:

SE  É O CONJUNTO VAZIO, ENTÃO

II) Sejam dois eventos e , onde  é complemento de , onde o espaço amostral   pode ser escrito da seguinte forma . Além disso, e  são mutuamente exclusivos. Sendo assim, teremos:

    

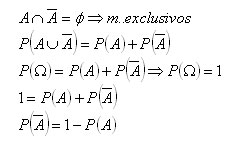
Se  é complemento de A, então

III) Se, por outro lado, tenho o seguinte conjunto , onde A e  são mutuamente exclusivos, teremos então:

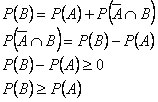
IV) Teorema da Soma: se A e B são dois eventos quaisquer, então: