Matemática Financeira
Módulo 7 - Juros Composto
Os juros compostos são conhecidos, popularmente, como "Juros sobre juros". |
7.1 - Introdução
Entendemos por juros compostos quando no final de cada período de capitalização, os rendimentos são incorporados ao capital, gerando um novo capital, sobre o qual serão calculados os rendimentos do período seguinte.
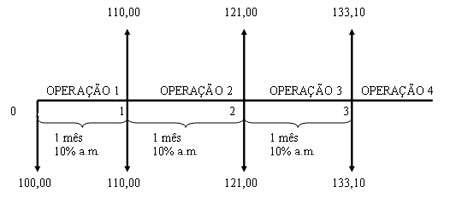
O regime de juros compostos é o mais comum no sistema financeiro e portanto, o mais útil para cálculos de problemas do dia-a-dia. Os juros gerados a cada período são incorporados ao principal para o cálculo dos juros do período seguinte.
Chamamos de capitalização o momento em que os juros são incorporados ao principal. Após três meses de capitalização, temos:
1º mês: M =C (1 + i)
2º mês: o principal é igual ao montante do mês anterior: M = C (1 + i) (1 + i)
3º mês: o principal é igual ao montante do mês anterior: M = C (1 + i) (1 + i) (1 + i)
Simplificando, obtemos a fórmula:
Importante: a taxa i tem que ser expressa na mesma medida de tempo de n, ou seja, taxa de juros ao mês para n meses.
Para calcularmos apenas os juros basta diminuir o principal do montante ao final do período:
A seguir são apresentados alguns exemplos sobre juros compostos. |
7.3 - Aplicações
7.3.1) Calcule o montante acumulado pela aplicação de um capital de R$ 6.000,00 aplicado a juros compostos, durante 1 ano, à taxa de 3,5% ao mês.
Solução:
C = R$ 6.000,00
t = 1 ano 
12 meses
i = 3,5 % ao mês 0,035
M = ?
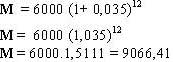
Resp. O montante acumulado é: $ 9.066,41
A taxa de juros está expressa ao mês e o prazo está ao ano, portanto devemos converter o prazo da operação para a mesma unidade de tempo. |
7.3.2) Determinar o valor atual de um contrato de R$ 30.000,00 com vencimento para 4 meses e através de uma taxa de juros de 3% ao mês, capitalizados mensalmente.
Solução:
M = R$ 30.000,00
t = 4 meses
i = 3 % a.m. 0,03
C = ?
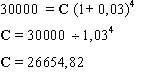
Resp. O valor atual do contrato é: $ 26.654,82
7.3.3) Uma loja financia um bem, no valor e R$ 4.200,00, sem entrada, para pagamento em uma única prestação de R$ 4.866,61 no final de 5 meses. Qual a taxa mensal cobrada pela loja?
Solução:
C = R$ 4.200,00
M = R$ 4.866,61
t = 5 meses
i = ? mensal
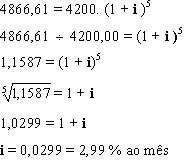
Resp. A taxa mensal de juros cobrada pela loja é: 2,99%
Normalmente em fatores ou índices calculados nas fórmulas são colocadas de quatro a seis casas decimais e os demais casos duas casas decimais! |
7.3.4) Determine em que prazo um empréstimo de R$ 10.000,00 pode ser quitado em um único pagamento de R$ 11.261,62, sabendo que a taxa contratada é de 2% ao mês.
Solução:
C = R$ 10.000,00
M = R$ 11.261,62
i = 2% ao mês 0,02
n = ?
Resp. O prazo contratado foi de: 6 meses
Em alguns livros de Matemática Financeira são colocadas Tabuas Financeiras com valores de exponenciais e logaritmos, apesar de hoje em dia ser muito comum o uso da calculadora HP 12C. |
7.4 - Fórmulas na HP 12C
Na fórmula , o principal C é também conhecido como Valor Presente
(PV = present value) e o montante M é também conhecido como Valor Futuro
(FV = future value). Então essa fórmula pode ser escrita como: 
Isolando PV na fórmula temos:
Com esta mesma fórmula podemos calcular o valor futuro a partir do valor presente. Na seqüência mais fórmulas que podemos obter diretamente cada elemento a partir dos dados iniciais do problema.
Na HP-12C, o valor presente é representado pela tecla PV e o valor futuro é representado pela tecla FV. |
É comum nas operações de curto prazo, onde predominam as aplicações com taxas referenciadas em juros simples, ter-se o prazo definido em número de dias. Nestes casos, o número de dias pode ser calculado de duas maneiras:
a) pelo tempo exato: utilizando-se efetivamente o calendário do ano civil (365 dias). O juro apurado desta maneira denomina-se juro exato;
b) pelo ano comercial: o qual admite o mês com 30 dias e o ano com 360 dias. Tem-se, por este critério, a apuração do denominado juro comercial ou ordinário.
Exemplo:
12% a.a. equivale, pelos critérios enunciados, à taxa diária de:
a) Juro Exato: 12/365 = 0,032877% a.d.
b) Juro Comercial: 12/360 = 0,033333% a.d.